Differenze tra le versioni di "Elusione"
| [versione bozza] | [versione verificata] |
(Respinta l'ultima modifica al testo (da MiSSiXTeen) e ripristinata la versione 41192 di Son Gohan: non oggettivate) |
|||
| (18 versioni intermedie di 4 utenti non mostrate) | |||
| Riga 1: | Riga 1: | ||
| − | + | {{... | |
| − | + | |Sezione=principale | |
| − | + | |Motivo=Non è ancora chiaro il ruolo dell'Elusione.}} | |
| − | + | ''Da non confondere con:'' '''[[Evasione]]'''. | |
| − | L' | + | L''''Elusione''' è uno dei [[parametri]] di un [[PG]]. La sua funzione, che si diceva consistere nel ridurre i danni subiti di una percentuale pari a metà del proprio valore, è stata smentita da [[DEX#Diminuzione del danno subìto|una scoperta riguardante la DEX]]. Ad oggi è dunque <u>'''del tutto ignota'''</u> la funzione dell'Elusione. |
| − | Salire sul [[Cavallo]] aumenta la DEX se questa è sotto un certo valore, quindi finché si è sul cavallo si ha un valore di Elusione superiore alla norma (a meno che non si abbia già la destrezza elevata). Il Cavallo Esperto fornisce | + | ==Aumentare l'Elusione== |
| + | |||
| + | L'unico modo per alzare i punti Elusione è alzare la [[Destrezza]]. 90 punti di DEX forniscono 30 punti Elusione, ma l'incremento fornito non è lineare, infatti più si [[Gergo di Metin#U|uppa]] DEX meno velocemente sale l'Elusione (vedi grafico a fine pagina). | ||
| + | |||
| + | Salire sul [[Cavallo]] aumenta la DEX se questa è sotto un certo valore, quindi finché si è sul cavallo si ha un valore di Elusione superiore alla norma (a meno che non si abbia già la destrezza elevata). Il [[Cavallo Esperto]] fornisce 26 punti di Elusione minimi. | ||
| + | |||
| + | ==Aumento dell'Elusione in funzione di DEX== | ||
| + | {| cellpadding="10" | ||
| + | | | ||
| + | {| {{Prettytable}} | ||
| + | |- | ||
| + | |{{Colore01}}|'''DEX''' | ||
| + | |{{Colore01}}|'''Elusione''' | ||
| + | |- | ||
| + | | 3 | ||
| + | | 3 | ||
| + | |- | ||
| + | | 4 | ||
| + | | 3 | ||
| + | |- | ||
| + | | 5 | ||
| + | | 4 | ||
| + | |- | ||
| + | | 6 | ||
| + | | 5 | ||
| + | |- | ||
| + | | 7 | ||
| + | | 5 | ||
| + | |- | ||
| + | | 8 | ||
| + | | 6 | ||
| + | |- | ||
| + | | 9 | ||
| + | | 6 | ||
| + | |- | ||
| + | | 10 | ||
| + | | 7 | ||
| + | |- | ||
| + | | 11 | ||
| + | | 7 | ||
| + | |- | ||
| + | | 12 | ||
| + | | 8 | ||
| + | |- | ||
| + | | 13 | ||
| + | | 8 | ||
| + | |- | ||
| + | | 14 | ||
| + | | 9 | ||
| + | |- | ||
| + | | 15 | ||
| + | | 9 | ||
| + | |- | ||
| + | | 16 | ||
| + | | 10 | ||
| + | |- | ||
| + | | 17 | ||
| + | | 10 | ||
| + | |- | ||
| + | | 18 | ||
| + | | 10 | ||
| + | |- | ||
| + | | 19 | ||
| + | | 11 | ||
| + | |- | ||
| + | | 20 | ||
| + | | 11 | ||
| + | |- | ||
| + | | 21 | ||
| + | | 12 | ||
| + | |- | ||
| + | | 22 | ||
| + | | 12 | ||
| + | |- | ||
| + | | 23 | ||
| + | | 12 | ||
| + | |- | ||
| + | | 24 | ||
| + | | 13 | ||
| + | |- | ||
| + | | 25 | ||
| + | | 13 | ||
| + | |- | ||
| + | | 26 | ||
| + | | 14 | ||
| + | |- | ||
| + | | 27 | ||
| + | | 14 | ||
| + | |- | ||
| + | | 28 | ||
| + | | 14 | ||
| + | |- | ||
| + | | 29 | ||
| + | | 15 | ||
| + | |- | ||
| + | | 30 | ||
| + | | 15 | ||
| + | |- | ||
| + | | 31 | ||
| + | | 15 | ||
| + | |- | ||
| + | | 32 | ||
| + | | 16 | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {| {{Prettytable}} | ||
| + | |- | ||
| + | |{{Colore01}}|'''DEX''' | ||
| + | |{{Colore01}}|'''Elusione''' | ||
| + | |- | ||
| + | | 33 | ||
| + | | 16 | ||
| + | |- | ||
| + | | 34 | ||
| + | | 16 | ||
| + | |- | ||
| + | | 35 | ||
| + | | 17 | ||
| + | |- | ||
| + | | 36 | ||
| + | | 17 | ||
| + | |- | ||
| + | | 37 | ||
| + | | 17 | ||
| + | |- | ||
| + | | 38 | ||
| + | | 18 | ||
| + | |- | ||
| + | | 39 | ||
| + | | 18 | ||
| + | |- | ||
| + | | 40 | ||
| + | | 18 | ||
| + | |- | ||
| + | | 41 | ||
| + | | 19 | ||
| + | |- | ||
| + | | 42 | ||
| + | | 19 | ||
| + | |- | ||
| + | | 43 | ||
| + | | 19 | ||
| + | |- | ||
| + | | 44 | ||
| + | | 20 | ||
| + | |- | ||
| + | | 45 | ||
| + | | 20 | ||
| + | |- | ||
| + | | 46 | ||
| + | | 20 | ||
| + | |- | ||
| + | | 47 | ||
| + | | 20 | ||
| + | |- | ||
| + | | 48 | ||
| + | | 21 | ||
| + | |- | ||
| + | | 49 | ||
| + | | 21 | ||
| + | |- | ||
| + | | 50 | ||
| + | | 21 | ||
| + | |- | ||
| + | | 51 | ||
| + | | 21 | ||
| + | |- | ||
| + | | 52 | ||
| + | | 22 | ||
| + | |- | ||
| + | | 53 | ||
| + | | 22 | ||
| + | |- | ||
| + | | 54 | ||
| + | | 22 | ||
| + | |- | ||
| + | | 55 | ||
| + | | 23 | ||
| + | |- | ||
| + | | 56 | ||
| + | | 23 | ||
| + | |- | ||
| + | | 57 | ||
| + | | 23 | ||
| + | |- | ||
| + | | 58 | ||
| + | | 23 | ||
| + | |- | ||
| + | | 59 | ||
| + | | 23 | ||
| + | |- | ||
| + | | 60 | ||
| + | | 24 | ||
| + | |- | ||
| + | | 61 | ||
| + | | 24 | ||
| + | |- | ||
| + | | 62 | ||
| + | | 24 | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {| {{Prettytable}} | ||
| + | |- | ||
| + | |{{Colore01}}|'''DEX''' | ||
| + | |{{Colore01}}|'''Elusione''' | ||
| + | |- | ||
| + | | 63 | ||
| + | | 24 | ||
| + | |- | ||
| + | | 64 | ||
| + | | 25 | ||
| + | |- | ||
| + | | 65 | ||
| + | | 25 | ||
| + | |- | ||
| + | | 66 | ||
| + | | 25 | ||
| + | |- | ||
| + | | 67 | ||
| + | | 25 | ||
| + | |- | ||
| + | | 68 | ||
| + | | 25 | ||
| + | |- | ||
| + | | 69 | ||
| + | | 26 | ||
| + | |- | ||
| + | | 70 | ||
| + | | 26 | ||
| + | |- | ||
| + | | 71 | ||
| + | | 26 | ||
| + | |- | ||
| + | | 72 | ||
| + | | 26 | ||
| + | |- | ||
| + | | 73 | ||
| + | | 26 | ||
| + | |- | ||
| + | | 74 | ||
| + | | 27 | ||
| + | |- | ||
| + | | 75 | ||
| + | | 27 | ||
| + | |- | ||
| + | | 76 | ||
| + | | 27 | ||
| + | |- | ||
| + | | 77 | ||
| + | | 27 | ||
| + | |- | ||
| + | | 78 | ||
| + | | 27 | ||
| + | |- | ||
| + | | 79 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 80 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 81 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 82 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 83 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 84 | ||
| + | | 28 | ||
| + | |- | ||
| + | | 85 | ||
| + | | 29 | ||
| + | |- | ||
| + | | 86 | ||
| + | | 29 | ||
| + | |- | ||
| + | | 87 | ||
| + | | 29 | ||
| + | |- | ||
| + | | 88 | ||
| + | | 29 | ||
| + | |- | ||
| + | | 89 | ||
| + | | 29 | ||
| + | |- | ||
| + | | 90 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 91 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 92 | ||
| + | | 30 | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {| {{Prettytable}} | ||
| + | |- | ||
| + | |{{Colore01}}|'''DEX''' | ||
| + | |{{Colore01}}|'''Elusione''' | ||
| + | |- | ||
| + | | 93 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 94 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 95 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 96 | ||
| + | | 30 | ||
| + | |- | ||
| + | | 97 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 98 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 99 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 100 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 101 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 102 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 103 | ||
| + | | 31 | ||
| + | |- | ||
| + | | 104 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 105 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 106 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 107 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 108 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 109 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 110 | ||
| + | | 32 | ||
| + | |- | ||
| + | | 111 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 112 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 113 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 114 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 115 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 116 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 117 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 118 | ||
| + | | 33 | ||
| + | |- | ||
| + | | 119 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 120 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 121 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 122 | ||
| + | | 34 | ||
| + | |- | ||
| + | |} | ||
| + | | | ||
| + | {| {{Prettytable}} | ||
| + | |- | ||
| + | |{{Colore01}}|'''DEX''' | ||
| + | |{{Colore01}}|'''Elusione''' | ||
| + | |- | ||
| + | | 123 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 124 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 125 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 126 | ||
| + | | 34 | ||
| + | |- | ||
| + | | 127 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 128 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 129 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 130 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 131 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 132 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 133 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 134 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 135 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 136 | ||
| + | | 35 | ||
| + | |- | ||
| + | | 137 | ||
| + | | 36 | ||
| + | |- | ||
| + | | 138 | ||
| + | | 36 | ||
| + | |- | ||
| + | | 139 | ||
| + | | 36 | ||
| + | |- | ||
| + | | 140 | ||
| + | | 36 | ||
| + | |- | ||
| + | | 141 | ||
| + | | 36 | ||
| + | |- | ||
| + | | 142 | ||
| + | | ? | ||
| + | |- | ||
| + | | 143 | ||
| + | | ? | ||
| + | |- | ||
| + | | 144 | ||
| + | | ? | ||
| + | |- | ||
| + | | 145 | ||
| + | | ? | ||
| + | |- | ||
| + | | 146 | ||
| + | | ? | ||
| + | |- | ||
| + | | 147 | ||
| + | | ? | ||
| + | |- | ||
| + | | 148 | ||
| + | | ? | ||
| + | |- | ||
| + | | 149 | ||
| + | | ? | ||
| + | |- | ||
| + | | 150 | ||
| + | | ? | ||
| + | |- | ||
| + | | 151 | ||
| + | | ? | ||
| + | |- | ||
| + | | 152 | ||
| + | | ? | ||
| + | |- | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | |||
| + | <center>'''Grafico dell'Elusione'''</center> | ||
| + | <center>[[File:GraficoElusione.jpg]]</center> | ||
| + | ===Osservazioni=== | ||
| + | Il grafico riporta il valore della [[Dex]] nell'asse delle ascisse e la corrispettiva elusione in quello delle ordinate; in nero è segnata una funzione polinomiale che ne approssima l'andamento. Appare evidente la non linearità della sua crescita, ma non si conosce l'esatta funzione che regola la sua crescita. | ||
[[Categoria:Info]] | [[Categoria:Info]] | ||
Versione attuale delle 21:18, 11 ott 2022
| Questa pagina è incompleta! | ||
Le informazioni presenti in questa pagina sono incomplete o non verificate. Contribuisci anche tu aiutandoci a verificarle!
|
Da non confondere con: Evasione.
L'Elusione è uno dei parametri di un PG. La sua funzione, che si diceva consistere nel ridurre i danni subiti di una percentuale pari a metà del proprio valore, è stata smentita da una scoperta riguardante la DEX. Ad oggi è dunque del tutto ignota la funzione dell'Elusione.
Aumentare l'Elusione
L'unico modo per alzare i punti Elusione è alzare la Destrezza. 90 punti di DEX forniscono 30 punti Elusione, ma l'incremento fornito non è lineare, infatti più si uppa DEX meno velocemente sale l'Elusione (vedi grafico a fine pagina).
Salire sul Cavallo aumenta la DEX se questa è sotto un certo valore, quindi finché si è sul cavallo si ha un valore di Elusione superiore alla norma (a meno che non si abbia già la destrezza elevata). Il Cavallo Esperto fornisce 26 punti di Elusione minimi.
Aumento dell'Elusione in funzione di DEX
|
|
|
|
|
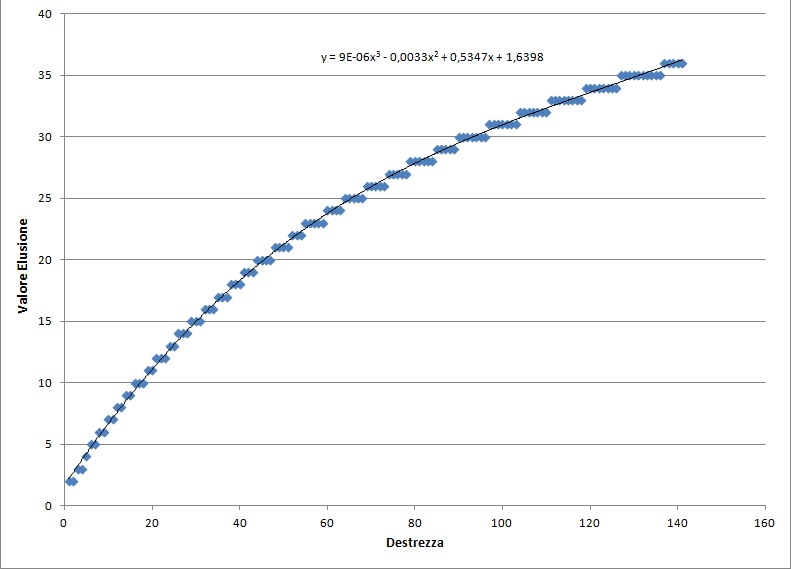
Osservazioni
Il grafico riporta il valore della Dex nell'asse delle ascisse e la corrispettiva elusione in quello delle ordinate; in nero è segnata una funzione polinomiale che ne approssima l'andamento. Appare evidente la non linearità della sua crescita, ma non si conosce l'esatta funzione che regola la sua crescita.